If `ax^(2) 2hxy by^(2) 2gx 2fy c = 0`, then `(dy)/(dx)` = Welcome to Doubtnut Doubtnut is World's Biggest Platform for Video Solutions of Physics, If ( 3, 2) lies on the circle x^2 y^2 2gx 2fy c = 0 which is concentric with the circle x^2 y^2 6x 8y – 5 = 0, then c = asked Jul 17 in Circles by Eeshta01 (This is the Solution of question from Cengage Publication Math Book Coordinate Geometry Chapter 6 CONIC SECTIONS written By G Tewani You can Find Solution

14 Circle Geometric Objects
Radius of circle x^2+y^2+2gx+2fy+c=0
Radius of circle x^2+y^2+2gx+2fy+c=0- x 2 y 2 2gx 2fy c = 0 (1) This equation may be written Hence (1) represents a circle whose centre is the point ( g, f), and whose radius is If g 2 f 2 > c, the radius of this circle is real If g 2 f 2 = c, the radius vanishes, i e the circle becomes a point coinciding with the point ( g, f) Such a circle is called a pointcircle Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
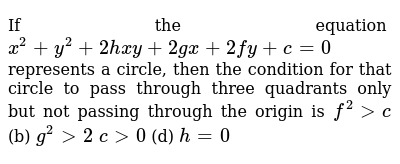



Prove That The Equation X2 Y2 2gx 2fy C 0 Always Represent
वृत्त `x^(2)y^(2)2gx 2fyc=0 ` द्वारा Y अक्ष पर काटागया अन्तः खंड `` है ।Click here👆to get an answer to your question ️ If the circle x^2 y^2 2gx 2fy c = 0 bisects the circumference of the circle x^2 y^2 2g1x 2f1y c1 = 0 , then the length of the common chord of the circles is খবর `x^(2)y^(2)2gx 2fyc=0 ` ওয়াই অক্ষের উপর ইন্টারডিজিটেশন `` হয়
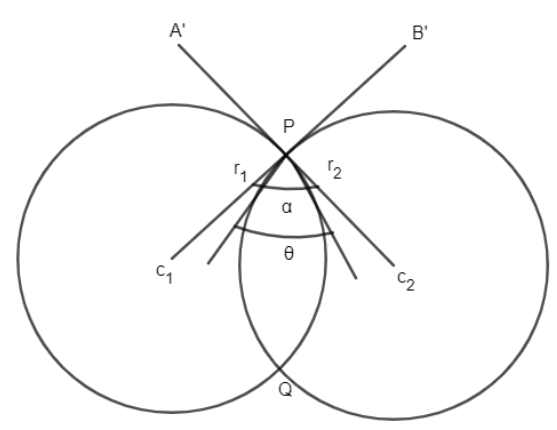
Given any second degree equation in $x$ and $y$, $ax^2by^22gx2fy2hxyc=0$ is it possible to find out the centre and/or the axis of the conic section it represents?Mathx^{2} y^{2} 2gx 2fy c =0/math math r = \sqrt{ g^{2} f^{2} c}/math Let S ≡ x 2 y 2 2gx 2fy c = 0 be a given circle Find the locus of the foot of the perpendicular drawn from the origin upon any chord of S which subtends a right angle at the origin
If the equation ax2 2hxy by2 2gx 2fy c = 0 represents a pair of intersecting lines, then show that the square of the distance of their point of intersection from the origin is 22 2 c(a b) f g ab h Also show that the square of this distance is 22Y = mx ± is always a tangent to the circle x 2 y 2 = a 2 whatever be the value of m The joint equation of a pair of tangents drawn from the point A (x1, y1) to the circle x2 y2 2gx 2fy c = 0 is T2 = SS1 The equation of the normal to the circle x 2 y 2 2gx 2fy c = 0 at any point (x 1, y 1) lying on the circle is The chords of the circle x^2 y^2 2gx 2fy 2c = 0 subtend right angle at the origin Show that the locus of the foot of the asked Oct




Math1 1




Prove That The Equation X2 Y2 2gx 2fy C 0 Always Represent
The Circle X2 Y2 2gx 2fy C = 0 Does Not Intersect Xaxis, If Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 11 Textbook Solutions 71 Important Solutions 3 Question Bank Solutions 51 Concept Notes & Videos 531 Syllabus Advertisement16 Given that the circle $$x^{2} y^{2} 2gx 2fy c = 0$$ touches the $y$axis, prove that $f^{2} = c$ So, because the circle touches the $y$axis, we knowClick here👆to get an answer to your question ️ If the two circles x^2 y^2 2gx 2fy = 0 and x^2 y^2 2g'x 2f'y = 0 touch each other, then show that f'g = fg'
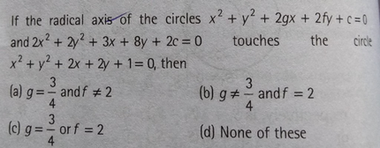



If The Radical Axis Of The Circles X2 Y2 2gx 2fy Cs And Scholr



If Tangents At Points X1 Y1 And X2 Y2 Of Circle X 2 Y 2 2gx 2fy C 0 Sarthaks Econnect Largest Online Education Community
To find xintercept made by the circle x 2 y 2 2gx 2fy c = 0, substitute y = 0 and get a quadratic equation in x, whose roots are, say, x 1 and x 2 These values represent the abscissae of ends A and B of x – intercept Length of x – intercept = AB = x 2 – x 1 Similarly, substituting x = 0, we get a quadratic equation in y whose roots, say, y 1 and y 2 are ordinates of Statement 1 If two circles x^2y^22gx2fy=0 and x^2y^22g^(prime)x2f^(prime)y=0 touch each other, then f^(prime)g=fg^(prime)dot Statement 2 Two circles touch other if the line joining their centers isClick here👆to get an answer to your question ️ If x^2 y^2 2gx 2fy 1 = 0 represents a pair of straight lines, then f^2 g^2 is equal to




If Xr Yr R 1 2 3 4 Be The Points Of Intersection Of The Parabola Y2 4ax And The Circle X2 Y2 2gx 2fy C 0 Then
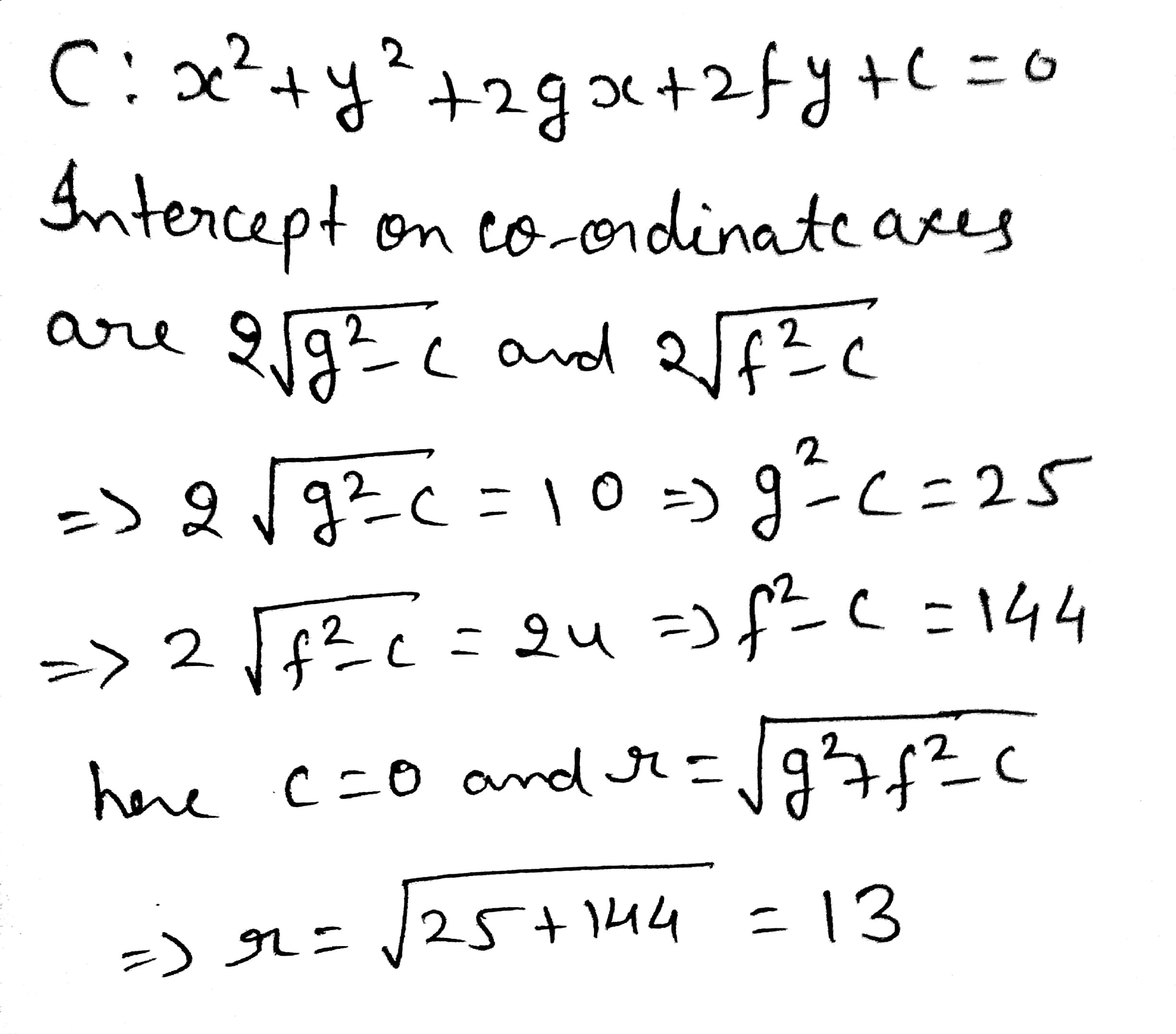



If The Lengths Of The Chords Intercepted By The Circle X 2 Y 2 2gx 2fy 0 From The Coordinate Axes Be 10 And 24 Respectively Then The Radius Of The Circle Is
The 2nd equation represents a surface in 3 dimensions Think about it this way For a given set of values for h,g and c , visit each point (x,y,z) in math\mathbb{R}^3 /mathand if the values x,y and z satisfy the equation, then darken the poiConcept The general second degree equation of a circle in x and y is given by a ⋅ x 2 a ⋅ y 2 2gx 2fy c = 0 with centre (g, f) and radius r = g 2 f 2 − c Calculation Given x 2 y 2 4x 2y 31 = 0 are equation of circle with centres C 1 and radius r 1If the two circles `x^(2)y^(2)2gxc=0` and `x^(2)y^(2)2fyc=0` have equal radius then locus of (g,f) is Welcome to Doubtnut Doubtnut is World's Biggest



Www Nextgurukul In Questions Answers Forum Question Academic Find Dydx




Ppt Mathematics Powerpoint Presentation Free Download Id
If the foci of the ellipse x 2 / 9 y 2 = 1 subtend right angle at a point P Then, the locus of P is If the force is given by F = at bt 2 with t as time The dimensions of a and b are If the fringe width is 04mm, the distance between the fifth bright and third dark band on the same side isवृत्त x 2 y 2 2gx 2fy c = 0 में बने एक समबाहु त्रिभुज का क्षेत्रफल है Free Practice With Testbook Mock Tests DSSSB TGT Maths Mock Test 21The general equation of a conic is as follows ax 2 2hxy by 2 2gx 2fy c = 0 where a, b, c, f, g, h are constants For a circle, a = b and h = 0 The equation becomes x 2 y 2 2gx 2fy c = 0(i) Given, x 2 y 2 x y = 0 Comparing with (i) we see that the equation represents a circle with 2g = 1
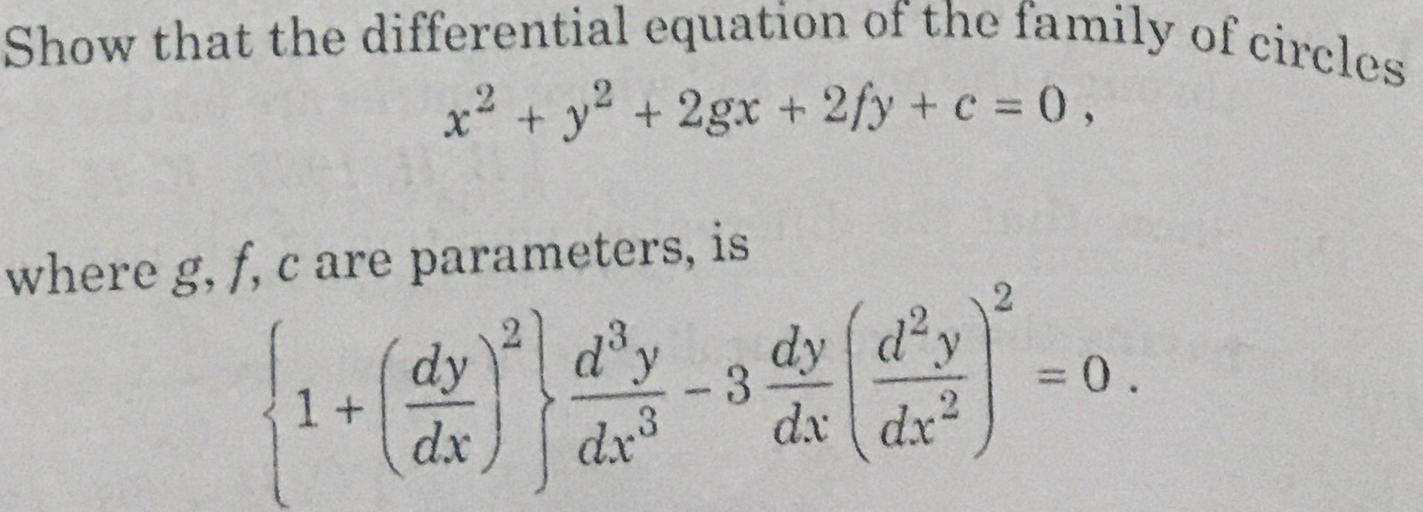



Show That The Differential Equation Of The Family Of Ci Math




The Equation X2 Y2 2gx 2fy C 0 Will Represent A Reai Circ Scholr
Updated On 32 To keep watching this video solution forLet (x 1, y 1) be any point on the circle x 2 y 2 2gx 2fy c = 0 Then, x 1 2 y 1 2 2gx 1 2fy 1 c = 0 ie x 1 2 y 1 2 2gx 1 2fy 1 = – c (i) Now, the length of the tangent from (x 1, y 1) to the circle x 2 y 2 2gx 2fy c 1 = c isGiven ax 2 2hxy by 2 2gx 2fy c = 0 (i) This represents pair of straight lines when abc 2fgh – af 2 – bg 2 – ch 2 = 0 (ii) When the pair of lines intersect y axis, x = 0 Put x = 0 in (i) by 2 2fy c = 0 This is a quadratic equation in y Since lines meet at yaxis, the roots must be equal So b 2 – 4ac = 0 => 4f 2




If The Pair Of Lines Ax2 2hxy By2 2gx 2fy C 0 Intersect On The Y Axis Thena 2fgh Bg2 Ch2b Bg2 Ne Ch2c Abc 2fghd None Of Thesecorrect



Let S X 2 Y 2 2gx 2fy C 0 Be A Given Circle Find The Locus Of The Foot Of The Perpendicular Sarthaks Econnect Largest Online Education Community
Correct answer If the circles x^2y^22gx2fyc=0 is touched by y=x at p to a circle passes through eanswersincomQuestion (View in English) समीकरण x 2 y 2 2gx 2fy c = 0 हमेशा एक वृत्त को दर्शाता है जिसका केंद्र (g, f) है और त्रिज्या है \(\sqrt {{g^2} {f^2} c} \)यदि g 2 f 2 = c, तो इस स्थिति में वृत्त क्या कहलाता है? (iv) If \(x^2 y^2 2gx 2fy c\) = 0, has three constants and to get the equation of the circle at least three conditions should be known \(\implies\) A unique circle passes through three noncollinear points Example Find the center and radius of the circle \(3x^2 3y^2 – 8x 10y 3\) = 0



If The Pair Of Lines Ax 2 2hxy By 2 2gx 2fy C 0 Intersect On The Y Axis Then Sarthaks Econnect Largest Online Education Community




Ppt Mathematics Powerpoint Presentation Free Download Id
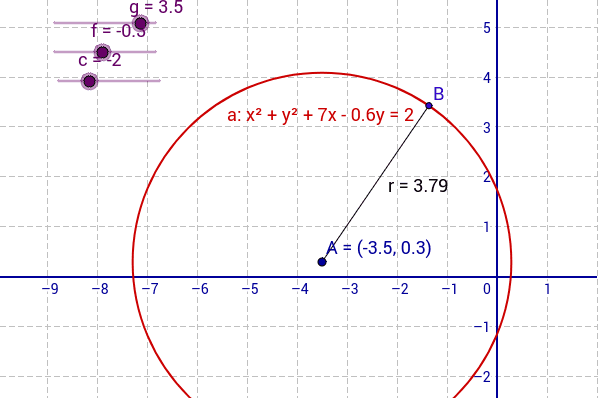
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSOLUTION Concept The Intercept made by the circle x 2 y 2 2gx 2fy c = 0 on I X –axis is given by \(2\sqrt {{g^2} c}\) II Y – axis is given by \(2\sqrt {{f^2} c}\) Note Intercepts are always positive Calculation Given Equation of circle x 2 y 2 4x – 7y 12 = 0 Now, by comparing the given equation of circle with the standard equation of circle x 2 y 2 You can clearly see the graph of a circle with the equation x^2 y^2 2gx2fyc=0 in red color If we change the values of f, g and c using their corresponding slide bars we will see that the position and size of the circle will change Let us observe how the size and position of the circle changes




2 Kea




If The Circle X2 Y2 2gx 2fy C 0 Passes Through All
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreClick here👆to get an answer to your question ️ If the circle x^2 y^2 2gx 2fy c = 0 cuts each of the circles x^2 y^2 4 = 0, x^2 y^2 6x 8y 10 = 0 and x^2 y^2 2x 4y 2 = 0 at the extremities of a diameter, thenIf the equation `ax^(2)2hxyby^(2)2gx2fyc=0` represents a pair of parallel lines, then



Find The Centre And Radius Of The Circles I X 2 Y 2 2gx 2fy C 0 Sarthaks Econnect Largest Online Education Community
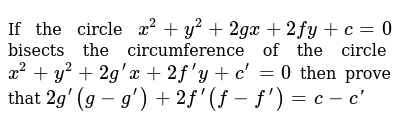



The Radical Axis Of The Circle X2 Y2 2gx 2fy C 0 And 2x
Click here👆to get an answer to your question ️ If the two circles x^2 y^2 2gx c = 0 and x^2 y^2 2fy c = 0 have equal radius then locus of (g , f) is2) f(x, y) = ax 2 2hxy by 2 2gx 2fy c = 0 which represents some conic located somewhere in the plane In Figure 1 a conic (an ellipse) is shown located at some point in the planeThis lesson will cover a few more examples on equations of circles Example 6 Find the centre and the radius of the circle x 2 y 2 – 4x 6y – 3 = 0 Solution Comparing this with the general equation of the circle, ie x 2 y 2 2gx 2fy c = 0, we have g = –2, f = 3 and c = – 3 The centre will be (–g, –f) or (2, –3), and the radius will be \( \sqrt{g^2f^2 – c} = \sqrt



The Chords Of The Circle X2 Y2 2gx 2fy 2c 0 Subtend Righ




If The Equation Ax2 2hxy By2 2gx 2fy C 0 Represents A Pair Of Straight Lines Then The Square Of The Brainly In
A circle is of the form x2 y2 2gx 2fy c = 0 and A circle is of the form x 2 y 2 2 g x 2 f y c = 0 and a pair of tangents are drawn from ( x 1 , y 1 ) to the circleThe combined equation of tangents is S S 1 = T 2Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




If The Cirde X2 Y2 2gx 2fy C 0 Touches X Axis Then A G F B G2 C C R C D G2 The Emiation Of The Circle Which Touches
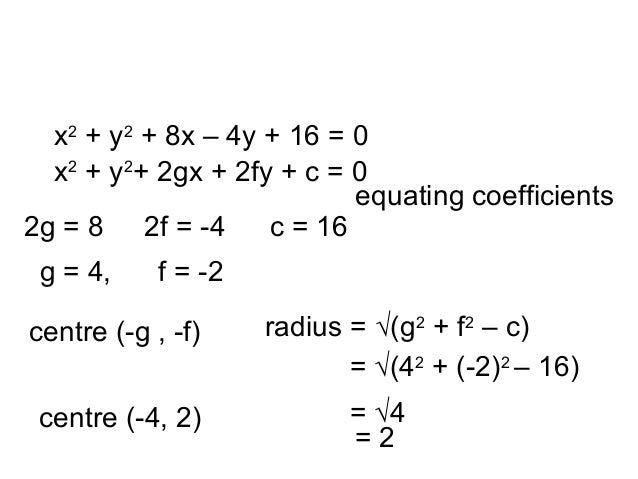



Circles Getting Centre And Radius 13
सर्कल द्वारा x अक्ष पर किए गए अवरोधन की लंबाई क्या है x^(2) y^(2) 2gx 2fy c = 0 ? The general equation of a circle is # x^2 y^2 2gx 2fy c = 0 # this circle has centre = (g , f ) and radius r = # sqrt(g^2f^2c) # the equation given here , compared with the general equation will give values of g and fSimple and best practice solution for ax^22hxyby^22gx2fyc=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it
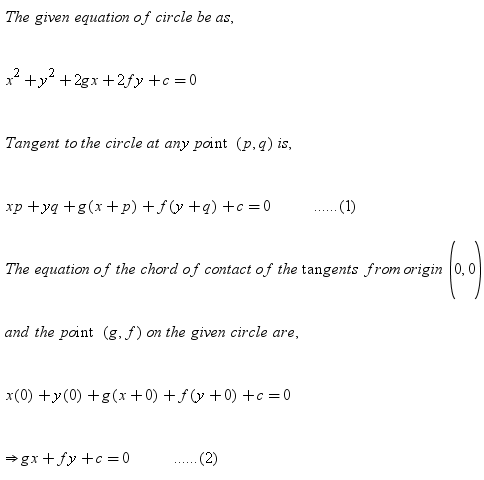



The Distance Between The Chords Of Contact Of Tangent To The Circle X Squared Y Squared 2 G X 2fy C 0 From The Origin And The Point G F Is




Circles
Show that the Points (3, −2), (1, 0), (−1, −2) and (1, −4) Are Concyclic




In The Equation X2 Y2 2gx 2fy C0 Represents A Circle Class 10 Maths Cbse




Find The Distance Between The Chords Of Contact Of The Tangent To The Circle X2 Y2 2gx 2fy C 0 From The Origin Maths Conic Sections Meritnation Com




X Square Y Square 2gx 2fy C 0 Find Dy Dx Maths Continuity And Differentiability Meritnation Com




Higherunit 2 Outcome 4 Circle X 2 Y 2 2gx 2fy C 0 The General Equation Of A Circle Wednesday 07 January Ppt Download



1




Higherunit 2 Outcome 4 Circle X 2 Y 2 2gx 2fy C 0 The General Equation Of A Circle Wednesday 07 January Ppt Download



4 A Square Is Inscribed In The Circle X2 Y2 2gx 2fy C 0 O




If Ax2 2hxy By2 2gx 2fy C 0 Find Dy Dx Brainly In



Q Tbn And9gcqla655 Pv5eh5fzivttclohrbxwkgx03q2pejeoefduywa6hm4 Usqp Cau




The Circle X 2 Y 2 2gx 2fy C 0 Does Not Intersect X A Xi S If G 2 Ltc B G 2 Gt C Youtube




Why The Equation Of Circle Is X 2 Y 2 2gx 2fy C 0 Where Did This Equation Came From Quora




Drive Equation X 2 Y 2 2gx 2fy C 0 Where Centre Points Of Circle Are G Maths Conic Sections Meritnation Com




Circles Getting Centre And Radius 13




Higherunit 2 Outcome 4 Circle X 2 Y 2 2gx 2fy C 0 The General Equation Of A Circle Wednesday 07 January Ppt Download




If The Cirde X2 Y2 2gx 2fy C 0 Touches X Axis Then A G F B G2 C C R C D G2 The Emiation Of The Circle Which Touches




If The Circle X 2 Y 2 2gx 2fy C 0 Cuts The Three Circl




The Centre Of Variable Circle X 2 Y 2 2gx 2fy C 0 Lies On The Line 2x 2y 9 0 An Youtube



Prove That The Equation X 2 Y 2 2gx 2fy C 0 Always Represents Sarthaks Econnect Largest Online Education Community




If From Any Point P On The Circle X 2 Y 2 2gx 2fy C 0 Tangents Are Drawn To The Circle X 2 Y 2 2gx 2fy C Sin 2 Alpha Left G 2 F 2 Right Cos 2 Alpha 0 Then The Angle Between The Tangents Is Snapsolve








Find The Area Of Equilateral Triangle Inscribed In A Circle X 2 Y 2 2gx 2fy C 0 Youtube



Find The Centre And Radius Of The Circles I X 2 Y 2 2gx 2fy C 0 Sarthaks Econnect Largest Online Education Community




Q22 If 3 2 Lies On The Circle X 2 Y 2 2gx 2fy C 0 Which Is Concentric With




Mathematics Notes



Statement 1 If The General Equation X Y 2xy 2gx Math




If The Circle X2 Y2 2gx 2fy C 0 Passes Through All The 4 Quadrants Then A G F B G F O C C O D Co



The Circle X2 Y2 2gx 2fy C 0 X A 2 Y B 2 R2 X2 Y2 R2 Ppt Download



Equation Of Circle X 2 Y 2 2gx 2fy C 0 Geogebra
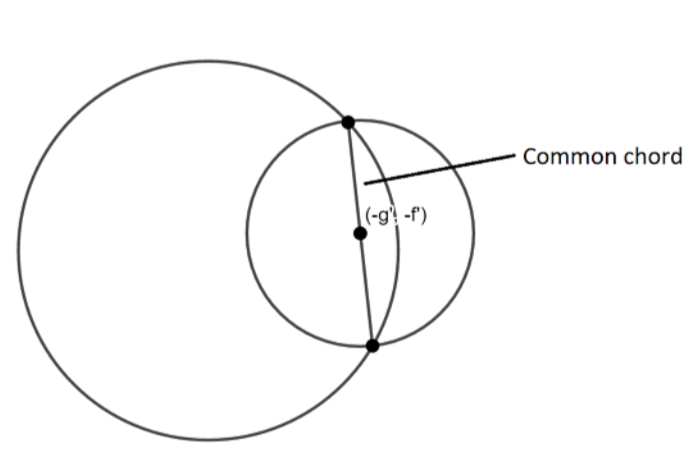



If The Circle X2 Y2 2gx 2fy C0 Bisects The Circumference Class 10 Maths Cbse
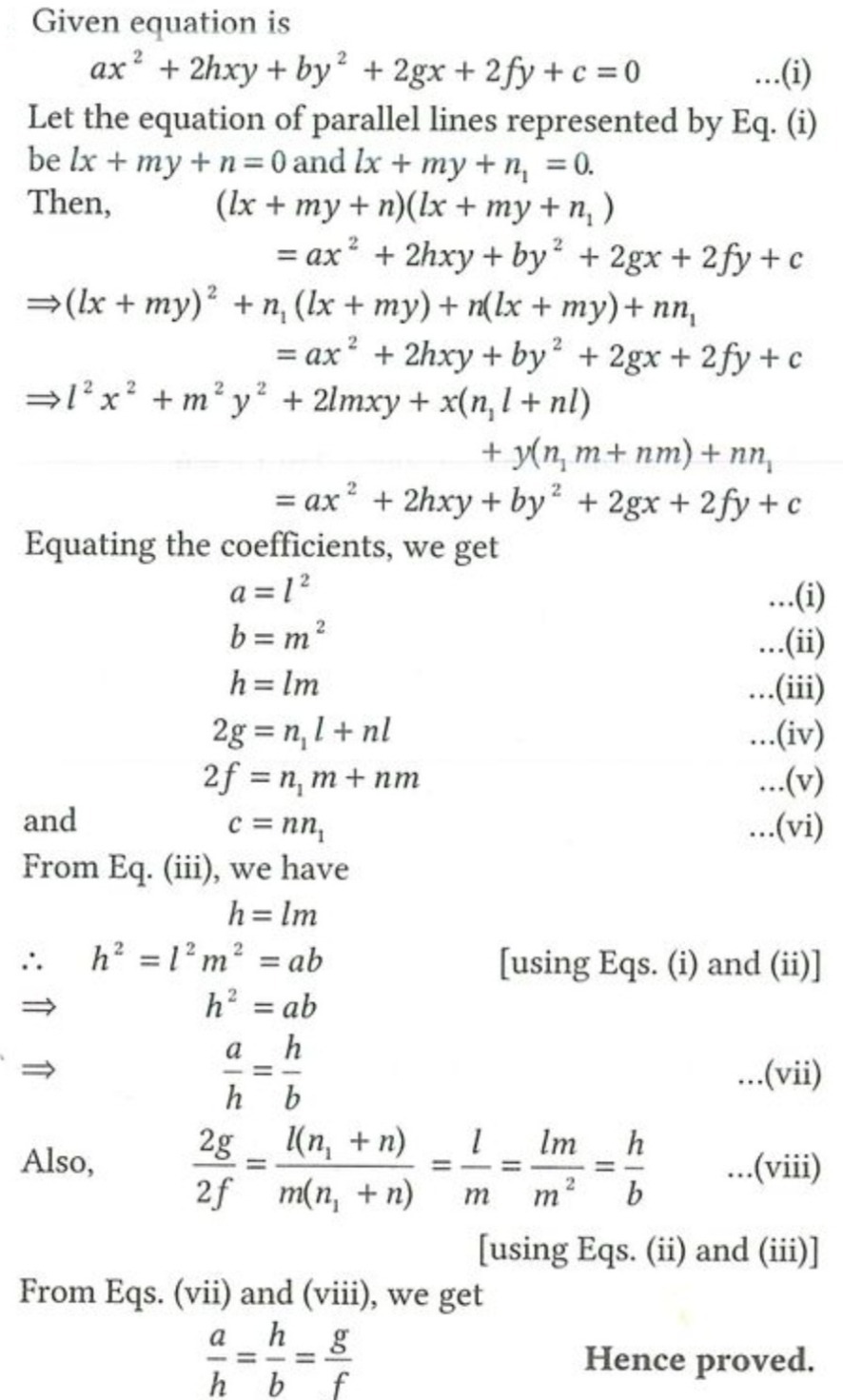



D If The Equation Ax2 2hxy By2 2gx 2fy C 0 Represe Gauthmath




If The Circle X 2 Y 2 2gx 2fy C 0 Touches X Axis Then



If From Any Point P On The Circle X 2 Y 2 2gx 2fy C 0 Tangents Are Drawn To The Circle X 2 Y 2 2gx 2fy C Sin 2 Alpha Left G 2 F 2 Right Cos 2 Alpha 0 Then Find The Angle Between The Tangents 0lt Alpha Lt



Show That The Length Of The Tangent From Any Point On The Circle X2 Y2 2gx 2fy C 0 To The Circle X2 Y2 2gx 2fy C1 0 Is




The Equation Ax 2 By 2 2hxy 2gx 2fy C 0 Represents A Circle Only If




Circles Part I Pdf Circle Cartesian Coordinate System
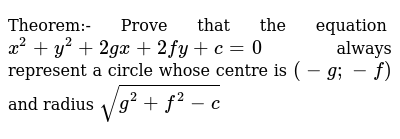



59 If The Equation X2 Y2 2gx 2fy C 0 Represents Acircle



The Radical Axis Of The Circle X2 Y2 2gx 2fy C 0 And 2x




14 Circle Geometric Objects



Algebraic Geometry A New Treatise On Analytical Conic Sections Pq Cv Is A Diameter Bisecting Chords Parallel To Pq Or Cv And Cv Pq Or Cv




Solved The Point X1y1 Lies Inside The Circle X2 Y2 2gx 2fy C 0 Self Study 365




If F2 G2 C Then The Equation X2 Y2 2gx 2fy C 0 Gauthmath




Consider The Family Of Circles X2 Y2 2fy 1 0 Where F Is A Parameter Thenthe Orthogonal Trajectories For This Family Is A X2 Y2 Dx 1




Solved If X1y1 Is A Point Inside The Circle X2 Y2 2gx 2fy C 0 Self Study 365




Solved A Given Circle X2 Y2 2gx 2fy C 0 Touches The X Self Study 365




A Circle X 2 Y 2 2gx 2fy C 0 Passes Through Three Co Normal Points On The Par Youtube



Let S X 2 Y 2 2gx 2fy C 0 Be A Given Circle Find The Locus Of The Foot Of The Perpendicular Sarthaks Econnect Largest Online Education Community




If From Any Point P On The Circle X 2 Y 2 2gx 2fy C 0 Tangents Are Drawn To The Circle X Youtube




If The Circle X 2 Y 2 2gx 2fy C 0 Touches By The Line Y X At The Point P Such That Op 6 2 Where




If The Circle X 2 Y 2 2gx 2fy C 0 Cuts The Three Circl



If The Two Circles X 2 Y 2 2gx C 0 And X 2 Y 2 2fy C 0 Have Equal Radius Then Locus Of Youtube



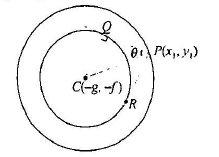
If O Is The Angle Subtended At P X Y By Thecircle S X2 Y2




Tangents Op And Oq Are Drawn From The Origin O To The Circle X2 Y2 2gx 2fy C Brainly In




Solved The Equation Of Tangent To The Circle X2 Y2 2gx 2fy C 0 Self Study 365



How The Conics Are Represented By The Quadratic Equation Math Ax 2 2hxy By 2 2gx 2fy C 0 Math Quora




If The Circle X 2 Y 2 2gx 2fy C 0 Bisects The Circumference Of The Circles X 2 Youtube



Prove That The Equation X2 Y2 2gx 2fy C 0 Always Represent



Find The Angle Of Intersection Of Two Circles X2 Y2 2gx 2fy C0 Class 10 Maths Cbse



Find Dy Dx When X And Y Are Connected By The Relation If Ax2 2hxy By2 2gx 2fy C 0 Then Show That Dy Dx Dx Dy 1 Studyrankersonline




Circles



1



1




If O Is The Origin And Op Oq Are Tangents To The Circle X 2 Y 2 2gx 2fy C 0 The Circumcentre Of The Triangle Opq Is




If Ax 2 2hxy By 2 2gx 2fy C 0 Then Show That Dy Dx Dx Dy 1 Youtube




5 If The Circle X 2 Y 2 2gx 2fy C 0 Touches X Axis At X 1




A Point A 2 1 Is Outside The Circles X 2 Y 2 2gx 2fy C 0 And Ap Maths Meritnation Com



Let Sequiv X 2 Y 2 2gx 2fy C 0 Be A Given Circle Find The Locus Of The Foot Of The Perpendicular Drawn From The Origin Upon Any Chord Of S Which Subtends A Right Angle




If The Two Circle X 2 Y 2 2gx C 0 And X 2 Y 2 2fy C Have Equal Radius Askiitians




Ppt Higher Unit 2 Powerpoint Presentation Free Download Id
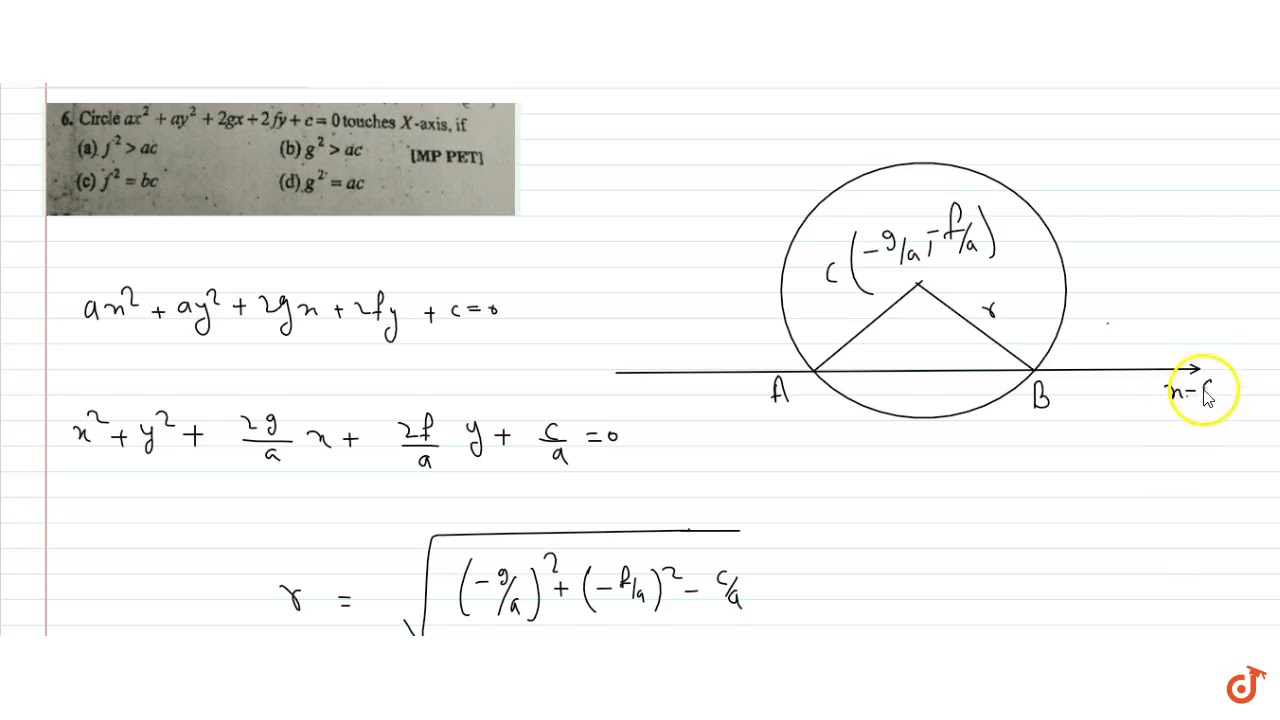



Circle Ax 2 Ay 2 2gx 2fy C 0 Touches X Axis If Youtube
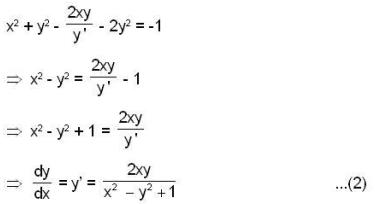



Consider The Family Of Circles X2 Y2 2fy 1 0 Where F Is A Parameter Thenthe Orthogonal Trajectories For This Family Is A X2 Y2 Dx 1



If Is The Angle Subtended At P X1 Y1 By The Circle S X2 Y2 2gx 2fy C 0 Then




A Find The Equation Of The Circle With Centre Chegg Com




If From Any Point P On The Circle X 2 Y 2 2gx 2fy C 0 Tangents Are Drawn To The Circle X 2 Y Youtube
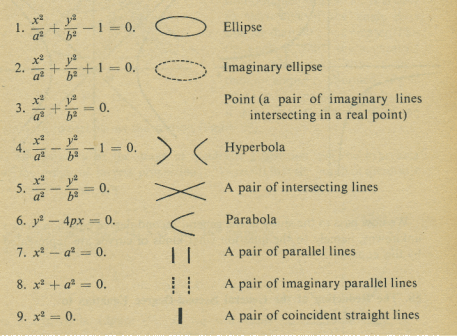



Analysis Of A Conic




Length Of The Tangent Drawn From Any Point X 2 Y 2 2gx 2fy C 0 To The Circle X 2 Y 2 2gx 2fy D 0 D C Is




04 A Prove That The Equation Of The Tangent Line At Chegg Com




X2 Y2 2gx 2fy C 0 E Find The Condition That The L Gauthmath




Solved If X2 Y2 2gx 2fy C 0 Intersects The X Axis At A Self Study 365




Correos Electronicos 12 Equation Of Pair Of Straight Lines Pdf Docer Com Ar




If Ax2 2hxy By2 2gx 2fy C 0 Find Dy Dx Brainly In



0 件のコメント:
コメントを投稿